AGRADECEMOS DE CORAZÓN  TU VISITA  A NUESTRO BLOG!!!

 

De parte de cada uno de los integrantes de este grupo les damos infinitas gracias a cada uno de nuestros visitantes, que con su acceso al blog han podido enriquecer aun mas su conocimiento, y el aporte que han observado dentro de este blog, que cada semana se publica algo nuevo e interesante pueda ser un aporte, un pequeño granito de arena para el gran potencial que cada uno de ustedes posee...

Lucinda Mishel Reyes Mérida

   Limbsei Dessire Gómez Félix

Raúl Avilio Carrillo Martínez

Estuardo Josué Alvarado Saucedo 

Martes 28 de Junio, 2022

 Operaciones con Conjuntos: 

Estas nos permiten realizar operaciones sobre los conjuntos para obtener otro conjunto.

entre ellos veremos Unión, Intersección, diferencia, diferencia simetrica y complemento. 

Unión de Conjuntos:

Es la unión de 2 o más conjuntos para formar a otro conjunto que contendra a todos los elementos que queremos unir pero sin que se repitan. puede ser un conjunto A y un conjunto B. la unión de los conjuntos A y B será otro conjunto formado por todos los elementos de A, con todos los elementos de B sin repetir ningún elemento. El símbolo que se usa para indicar la operación de unión es el siguiente: U. Cuando usamos diagramas de Venn, para representar la unió de conjuntos, se sombrean los conjuntos que se unen o se forma uno nuevo. Luego se escribe por fuera la operación de unión. 

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9,10,11}. Usando diagramas de Venn se tendría lo siguiente:

También se puede graficar del siguiente modo:

Intersección de Conjuntos:

 Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos. El símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}. Usando diagramas de Venn se tendría lo siguiente:

Diferencia de Conjuntos:   

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir dados dos conjuntos A y B, la diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El símbolo que se usa para esta operación es el mismo que se usa para la resta o sustracción, que es el siguiente. 

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será A-B={1,2,3}. Usando diagramas de Venn se tendría lo siguiente:

Diferencia Simetrica:  

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no comunes a los conjuntos A y B. El símbolo que se usa para indicar la operación de diferencia simétrica es el siguiente: △.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

Complemento de un Conjunto: 

Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no están en el conjunto. Es decir dado un conjunto A que esta incluido en el conjunto universal U, entonces el conjunto complemento de A es el conjunto formado por todos los elementos del conjunto universal pero sin considerar a los elementos que pertenezcan al conjunto A. En esta operación el complemento de un conjunto se denota con un apostrofe sobre el conjunto que se opera, algo como esto A' en donde el el conjunto A es el conjunto del cual se hace la operación de complemento.

Ejemplo 1.

Dado el conjunto Universal U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los siguientes elementos A'={3,4,5,6,7,8}. Usando diagramas de Venn se tendría lo siguiente:

Martes 28 de Junio, 2022

 

Conjuntos: conceptos, notación y formas de representación. Conjunto universo y complemento. 

Un conjunto:  

es una colección de objetos. Los objetos que pertenecen al conjunto se llaman elementos, o miembros, del conjunto. Los conjuntos se definen usando cualquiera de los tres métodos siguientes:
 l. descripción con palabras,
2. método de listado y
3. notación de comprensión. 

 El conjunto de números naturales pares menores que 10
 {2, 4, 6, 8}
{xlx es un número natural par menor que 10}

La notación de comprensión de arriba se lee como "el conjunto de todas las x donde x es un número natural par menor que 10". La notación de comprensión utiliza la idea algebraica de variable. (Se podría utilizar cualquier símbolo, pero, al igual que en otras aplicaciones algebraicas, la letra x es una selección común). 

 + {xlx es w1 número natural par menor que 10 }
A los conjuntos normalmente se les asigna un nombre (usualmente con letras mayúsculas), como E para el conj unto de todas las letras del abecedario inglés.

 E = { a, b, c, d, e, f, g, h, i, j, k, 1, m, n, o, p, q, r, s, t, u, v, w, x, y, z}

La notación de listado con frecuencia se abrevia estableciendo el patrón de elementos incluidos y utilizando puntos suspensivos para indicar la continuación del patrón. 

E= {a, b, c, d, ... , x, y, z} o E= { a, b, c, d, e, ... , z}. 

Un conjunto que no contiene elementos se llama conjunto vacío, o conjunto nuJo. El símbolo � se usa para denotar un conj unto vacío, de modo que 0 y D tienen el mismo significado. No identificamos el conj w1to vacío como {0} porque esta notación representaría a un conj unto con un elemento (ese elemento es el conjunto vacío). 

Clases de Conjuntos: 

Conjuntos Finitos: 

son aquellos a los que se le puede asignar un valor. 

Ejemplo: 

B= { Vocales } 

B= { a, e, i, o, u }

Conjuntos Infinitos: 

son aquellos que no se les puede asignar un valor. 

Ejemplo: 

C= { los números primos Positivos }

Conjunto Unitario: 

Ejemplo: 

A= {x|x E N, 3< x < 4}

A= {4} 

Conjunto Vacio:

{ }

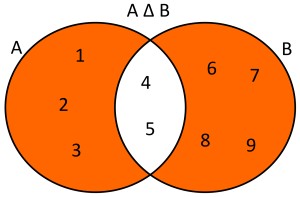
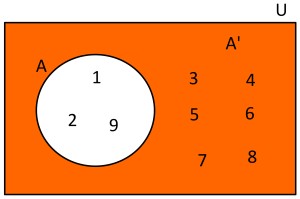
Conjunto Complementario: 

es el que va a determinar los elementos que faltan en el conjunto. 

Ejemplo: 

J= {0, 1, 2, 7  }

G= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} 

Á = { 3, 4, 5, 6, 8, 9} 

 CLASE SESION 4 

23/06/2022

Durante la sesión analizamos cada uno de los contenidos anteriores sobre el Webinario virtual al que nos conectamos todos los estudiantes de la facultad de ciencias económicas y empresariales, luego se dejo realizar una infografía de los puntos mas importantes de este tema que era AGEXPORT, como a continuación puedes observarlo. 

DG👽

23 de junio, Sesión 3 " Webinario AGEXPORT "🤑

 Webinario AGEXPORT

En la primera sesión del día, tuvimos un webinario de AGEXPORT, ahora se preguntara, quien es o que es AGEXPORT?

Para empezar AGEXPORT es una asociación privada sin fines de lucro, que busca ayudar a los comercios guatemaltecos a alcanzar el nivel de exportación internacional para beneficiar la economía guatemalteca y las divisas extranjeras para un crecimiento en el país.

Debido al gran tiempo de su existencia poseen experiencia en el campo además de buenos resultados en el campo de acción, como por ejemplo, en los productos de exportación mayoritarios en Guatemala de un periodo a otro, vemos aquí una grafica de exportaciones en Guatemala antes de AGEXPORT.

Y la grafica después de que AGEXPORT fuera creada y tuviera un impacto hizo que la economia diera un gran giro, y puede comprobarlo en esta grafica:

Y al ver estos resultados podemos intuir en los beneficios de esta asociación, cabe decir que AGEXPORT usa además datos de ingresos anuales en Guatemala, ósea de que fuentes en su mayoría constituyen los ingresos al país, para usarlos en estadística y probabilidades en su día  a día como agencia exportadora, este es un ejemplo de eso: 

Sin mas, queda decir que mi opinión de este webinario es positiva ya que conocimos una agencia que trae varios beneficios para el país y ayuda a el crecimiento del mercado en Guatemala, un mercado que ahora es interconectado y globalizado, sin mas fue una sesión de mucho aprendizaje :).

-EJ 

Martes 21 de Junio, 2022

 

Formas de la condicional: Converso, Inverso, y contrapositivo.❤
Formas alternativas de la condicional. Bicondicional.

Condicional: son proposiciones de la forma "si p entonces q" (p --> q).

Ejemplo:

1. Si ella entrega la tarea, entonces aprueba el curso.

p: ella entrega la tarea. 

q: aprueba el curso.

Connverso de la condicional:  son proposiciones de la forma "si q entonces p" (q --> p). 

Ejemplo:

1. si ella aprueba el curso entonces entregó la tarea.

Inversa: son proposiciones de la forma " si no p entonces no q".   (~p --> ~q).

Ejemplo:

1. Si ella no entrega la tarea entonces no aprueba el cuerso.

Contrapositivo: son proposiciones de la forma "si no q entonces no p".  (~q --> ~p).

 

Ejemplo: 

1. si no aprueba el curso entonces no entregó la tarea. 

BICONDICIONAL: son proposiciones de la forma "p si y solo si q".  (p <--> q).

Ejemplo:

p: un polígono es un cuadrilátero.

q: tiene 4 lados.

p <--> q

1. un plígono es un cuadrilátero si solo si tiene 4 lados.

2. un número es par, si solo si es divisible por 2. 

Martes 21 de Junio 2022

 

Negación de la condicional. Enunciados equivalentes a partir de la condicional

En la seción del día martes 21 de junio, los participantes antes de la seción leyeron las paginas del Nlibro Miller" para tener la base de lo que se iba a trabajar en cclase y asi mismo poder elaborar los ejericios de dicho libro. 

siendo las páginas 43,44,45, 46 y 47 las principales de esta lectura para poder elavorar las distintas tareas asignadas por el catedrático.