Martes 28 de Junio, 2022

 Operaciones con Conjuntos: 

Estas nos permiten realizar operaciones sobre los conjuntos para obtener otro conjunto.

entre ellos veremos Unión, Intersección, diferencia, diferencia simetrica y complemento. 

Unión de Conjuntos:

Es la unión de 2 o más conjuntos para formar a otro conjunto que contendra a todos los elementos que queremos unir pero sin que se repitan. puede ser un conjunto A y un conjunto B. la unión de los conjuntos A y B será otro conjunto formado por todos los elementos de A, con todos los elementos de B sin repetir ningún elemento. El símbolo que se usa para indicar la operación de unión es el siguiente: U. Cuando usamos diagramas de Venn, para representar la unió de conjuntos, se sombrean los conjuntos que se unen o se forma uno nuevo. Luego se escribe por fuera la operación de unión. 

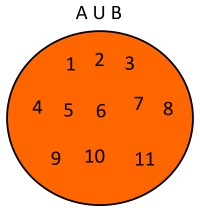
Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9,10,11}. Usando diagramas de Venn se tendría lo siguiente:

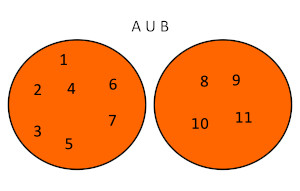
También se puede graficar del siguiente modo:

Intersección de Conjuntos:

 Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos. El símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.

Ejemplo 1.

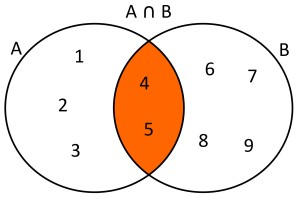
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}. Usando diagramas de Venn se tendría lo siguiente:

Diferencia de Conjuntos:   

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir dados dos conjuntos A y B, la diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El símbolo que se usa para esta operación es el mismo que se usa para la resta o sustracción, que es el siguiente. 

Ejemplo 1.

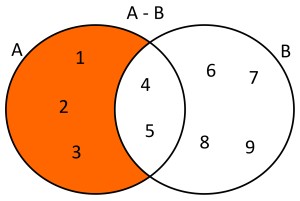
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será A-B={1,2,3}. Usando diagramas de Venn se tendría lo siguiente:

Diferencia Simetrica:  

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no comunes a los conjuntos A y B. El símbolo que se usa para indicar la operación de diferencia simétrica es el siguiente: △.

Ejemplo 1.

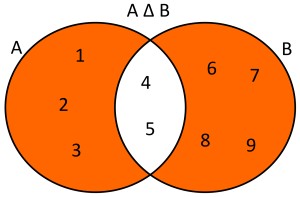
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

Complemento de un Conjunto: 

Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no están en el conjunto. Es decir dado un conjunto A que esta incluido en el conjunto universal U, entonces el conjunto complemento de A es el conjunto formado por todos los elementos del conjunto universal pero sin considerar a los elementos que pertenezcan al conjunto A. En esta operación el complemento de un conjunto se denota con un apostrofe sobre el conjunto que se opera, algo como esto A' en donde el el conjunto A es el conjunto del cual se hace la operación de complemento.

Ejemplo 1.

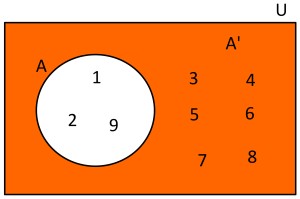
Dado el conjunto Universal U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los siguientes elementos A'={3,4,5,6,7,8}. Usando diagramas de Venn se tendría lo siguiente: