Martes 28 de Junio, 2022

 Operaciones con Conjuntos: 

Estas nos permiten realizar operaciones sobre los conjuntos para obtener otro conjunto.

entre ellos veremos Unión, Intersección, diferencia, diferencia simetrica y complemento. 

Unión de Conjuntos:

Es la unión de 2 o más conjuntos para formar a otro conjunto que contendra a todos los elementos que queremos unir pero sin que se repitan. puede ser un conjunto A y un conjunto B. la unión de los conjuntos A y B será otro conjunto formado por todos los elementos de A, con todos los elementos de B sin repetir ningún elemento. El símbolo que se usa para indicar la operación de unión es el siguiente: U. Cuando usamos diagramas de Venn, para representar la unió de conjuntos, se sombrean los conjuntos que se unen o se forma uno nuevo. Luego se escribe por fuera la operación de unión. 

Ejemplo 1.

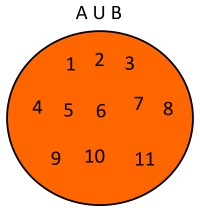
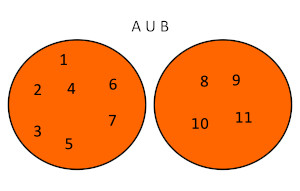
Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9,10,11}. Usando diagramas de Venn se tendría lo siguiente:

También se puede graficar del siguiente modo:

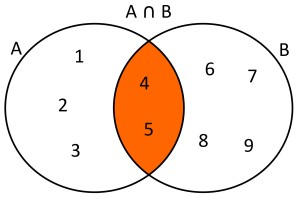
Intersección de Conjuntos:

 Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos. El símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}. Usando diagramas de Venn se tendría lo siguiente:

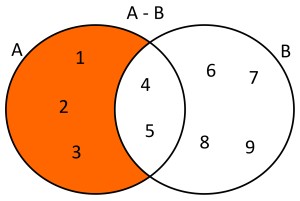
Diferencia de Conjuntos:   

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir dados dos conjuntos A y B, la diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El símbolo que se usa para esta operación es el mismo que se usa para la resta o sustracción, que es el siguiente. 

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será A-B={1,2,3}. Usando diagramas de Venn se tendría lo siguiente:

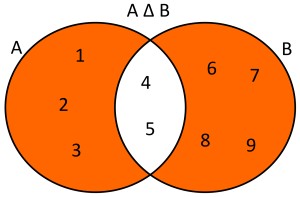
Diferencia Simetrica:  

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no comunes a los conjuntos A y B. El símbolo que se usa para indicar la operación de diferencia simétrica es el siguiente: △.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

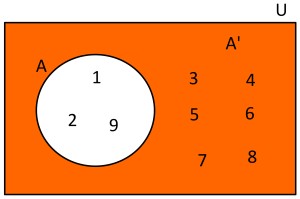
Complemento de un Conjunto: 

Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no están en el conjunto. Es decir dado un conjunto A que esta incluido en el conjunto universal U, entonces el conjunto complemento de A es el conjunto formado por todos los elementos del conjunto universal pero sin considerar a los elementos que pertenezcan al conjunto A. En esta operación el complemento de un conjunto se denota con un apostrofe sobre el conjunto que se opera, algo como esto A' en donde el el conjunto A es el conjunto del cual se hace la operación de complemento.

Ejemplo 1.

Dado el conjunto Universal U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los siguientes elementos A'={3,4,5,6,7,8}. Usando diagramas de Venn se tendría lo siguiente:

Martes 28 de Junio, 2022

 

Conjuntos: conceptos, notación y formas de representación. Conjunto universo y complemento. 

Un conjunto:  

es una colección de objetos. Los objetos que pertenecen al conjunto se llaman elementos, o miembros, del conjunto. Los conjuntos se definen usando cualquiera de los tres métodos siguientes:
 l. descripción con palabras,
2. método de listado y
3. notación de comprensión. 

 El conjunto de números naturales pares menores que 10
 {2, 4, 6, 8}
{xlx es un número natural par menor que 10}

La notación de comprensión de arriba se lee como "el conjunto de todas las x donde x es un número natural par menor que 10". La notación de comprensión utiliza la idea algebraica de variable. (Se podría utilizar cualquier símbolo, pero, al igual que en otras aplicaciones algebraicas, la letra x es una selección común). 

 + {xlx es w1 número natural par menor que 10 }
A los conjuntos normalmente se les asigna un nombre (usualmente con letras mayúsculas), como E para el conj unto de todas las letras del abecedario inglés.

 E = { a, b, c, d, e, f, g, h, i, j, k, 1, m, n, o, p, q, r, s, t, u, v, w, x, y, z}

La notación de listado con frecuencia se abrevia estableciendo el patrón de elementos incluidos y utilizando puntos suspensivos para indicar la continuación del patrón. 

E= {a, b, c, d, ... , x, y, z} o E= { a, b, c, d, e, ... , z}. 

Un conjunto que no contiene elementos se llama conjunto vacío, o conjunto nuJo. El símbolo � se usa para denotar un conj unto vacío, de modo que 0 y D tienen el mismo significado. No identificamos el conj w1to vacío como {0} porque esta notación representaría a un conj unto con un elemento (ese elemento es el conjunto vacío). 

Clases de Conjuntos: 

Conjuntos Finitos: 

son aquellos a los que se le puede asignar un valor. 

Ejemplo: 

B= { Vocales } 

B= { a, e, i, o, u }

Conjuntos Infinitos: 

son aquellos que no se les puede asignar un valor. 

Ejemplo: 

C= { los números primos Positivos }

Conjunto Unitario: 

Ejemplo: 

A= {x|x E N, 3< x < 4}

A= {4} 

Conjunto Vacio:

{ }

Conjunto Complementario: 

es el que va a determinar los elementos que faltan en el conjunto. 

Ejemplo: 

J= {0, 1, 2, 7  }

G= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} 

Á = { 3, 4, 5, 6, 8, 9} 

 CLASE SESION 4 

23/06/2022

Durante la sesión analizamos cada uno de los contenidos anteriores sobre el Webinario virtual al que nos conectamos todos los estudiantes de la facultad de ciencias económicas y empresariales, luego se dejo realizar una infografía de los puntos mas importantes de este tema que era AGEXPORT, como a continuación puedes observarlo. 

DG👽

23 de junio, Sesión 3 " Webinario AGEXPORT "🤑

 Webinario AGEXPORT

En la primera sesión del día, tuvimos un webinario de AGEXPORT, ahora se preguntara, quien es o que es AGEXPORT?

Para empezar AGEXPORT es una asociación privada sin fines de lucro, que busca ayudar a los comercios guatemaltecos a alcanzar el nivel de exportación internacional para beneficiar la economía guatemalteca y las divisas extranjeras para un crecimiento en el país.

Debido al gran tiempo de su existencia poseen experiencia en el campo además de buenos resultados en el campo de acción, como por ejemplo, en los productos de exportación mayoritarios en Guatemala de un periodo a otro, vemos aquí una grafica de exportaciones en Guatemala antes de AGEXPORT.

Y la grafica después de que AGEXPORT fuera creada y tuviera un impacto hizo que la economia diera un gran giro, y puede comprobarlo en esta grafica:

Y al ver estos resultados podemos intuir en los beneficios de esta asociación, cabe decir que AGEXPORT usa además datos de ingresos anuales en Guatemala, ósea de que fuentes en su mayoría constituyen los ingresos al país, para usarlos en estadística y probabilidades en su día  a día como agencia exportadora, este es un ejemplo de eso: 

Sin mas, queda decir que mi opinión de este webinario es positiva ya que conocimos una agencia que trae varios beneficios para el país y ayuda a el crecimiento del mercado en Guatemala, un mercado que ahora es interconectado y globalizado, sin mas fue una sesión de mucho aprendizaje :).

-EJ 

Martes 21 de Junio, 2022

 

Formas de la condicional: Converso, Inverso, y contrapositivo.❤
Formas alternativas de la condicional. Bicondicional.

Condicional: son proposiciones de la forma "si p entonces q" (p --> q).

Ejemplo:

1. Si ella entrega la tarea, entonces aprueba el curso.

p: ella entrega la tarea. 

q: aprueba el curso.

Connverso de la condicional:  son proposiciones de la forma "si q entonces p" (q --> p). 

Ejemplo:

1. si ella aprueba el curso entonces entregó la tarea.

Inversa: son proposiciones de la forma " si no p entonces no q".   (~p --> ~q).

Ejemplo:

1. Si ella no entrega la tarea entonces no aprueba el cuerso.

Contrapositivo: son proposiciones de la forma "si no q entonces no p".  (~q --> ~p).

 

Ejemplo: 

1. si no aprueba el curso entonces no entregó la tarea. 

BICONDICIONAL: son proposiciones de la forma "p si y solo si q".  (p <--> q).

Ejemplo:

p: un polígono es un cuadrilátero.

q: tiene 4 lados.

p <--> q

1. un plígono es un cuadrilátero si solo si tiene 4 lados.

2. un número es par, si solo si es divisible por 2. 

Martes 21 de Junio 2022

 

Negación de la condicional. Enunciados equivalentes a partir de la condicional

En la seción del día martes 21 de junio, los participantes antes de la seción leyeron las paginas del Nlibro Miller" para tener la base de lo que se iba a trabajar en cclase y asi mismo poder elaborar los ejericios de dicho libro. 

siendo las páginas 43,44,45, 46 y 47 las principales de esta lectura para poder elavorar las distintas tareas asignadas por el catedrático.

Jueves 16 de junio. Sesión 3: " Conjunción y disyunción" 🤓

 Conjunción y disyunción

Antes de la sesión tuvimos material que nos iba a dar una idea básica del tema para ir a la clase con algunos conceptos ya en mente

Al momento de trabajar preposiciones ya sean verdaderas o falsas existen las conjunciones y disyunciones que son ciertos caracteres que modifican los resultados de las oraciones y cambian algunas frases en las oraciones, estas dos son parte de el grupo de Los conectivos lógicos.

Aquí un ejemplo de la conjunción:

Y un ejemplo de la disyunción: 

Cada una de estas posee una tabla de valores que nos ayudara a orientarnos de  cuando un enunciado ya sea en conectivo de conjunción o conectivo de disyunción es verdadera o falsa.

En la conjunción la tabla es:

Y en la disyunción es

Fue un tema simple de ver, además de que trabajamos en equipos para discutir ideas o hacer alguna actividad para poder entender el tema al máximo, además de la ayuda del profesor por si nos surgía dudas con el tema presentado.

No tengo recomendación o idea alguna para compartir con este tema, creo que las actividades hechas y propuestas en la clase son suficiente para entender el tema a plenitud completa.

-EJ

Martes 14 de junio, 2022

 Proposiciones y valores de verdad. Negación

es una idea o enunciado, que tiene un valor de verdad y se representan con las letras de la p hasta la z. pueden ser verdaderas o falsas. 

Ejemplos:

p: el 17 es numero primo. 

p: El mundo es redondo.

p: 3 es mayor a 4. 

hay 2 tipos de proposiciones estan las Proposiciones abiertas y las Proposiciones cerradas. 

Proposiciones Abiertas: es un enunciado que no se puede calificar como verdadero o falso, por lo tanto no tiene valor de verdad. 

ejemplos:

- Él juega futbol.

- 3 + y = 21.

- Ella esta en tercer grado.

Proposiciones Cerradas: es un enunciado que se califica directamente como verdadero o falso.

Ejemplos:

p: Todos los humanos son mortales.  (v)

Expresiones no Proporcionales: son a aquellos que no se les puede asignar un valor de verdad.

Ejemplos:

1. exclamaciones como: ¡Bienvenidos!
2. Interrogaciones: ¿Cuantas ventas hubo?
3. Imperativos como: pásame eso
4. Opiniones.

NEGACIÓN DE LA PROPOSICIÓN.

Es negar la proposición como la negación de una proposición verdadera, es una falsa.

Ejemplo:

proposicion de verdad:
1. Plutón no es un planeta.

Negación de la proposición:
1. Plutón es un Planeta.

y la negación de una proposición falsa, es una verdadera.

Ejemplo:

proposición de verdad:
2. Para ser diputado se tiene que estar graduando a nivel universitario.

Negación de la proposición:
2. Para ser diputado no se tiene que estar graduado a nivel universitario.

Prueba Sumativa II Martes 14 de Junio 2022.

 Prueba Sumativa II

En la primera secion del día martes 14 de junio del 2022, los participantes hicieron la respectivba prueba sumatiba, en la que tubieron que elavorar y poner en practica los diferentes temas vistos durante las seciones.

Jueves 9 de junio, sesión 4: Interpretación de otro tipo de gráficos.

 Interpretación de otros tipos de gráficas

Las graficas circulares son muy usadas hoy en día, pero esta la existencia de mas gráficos para los análisis estadísticos o económicos, dependiendo de su contexto, podemos encontrar varios ejemplos por medio del link que nos da la misma plataforma.

Al utilizar este link encontrábamos varios tipos de gráficos:

Como vemos, los gráficos tienen una gran variedad de interpretaciones y de usos, normalmente los mas usados son los circulares o los de barras por su fácil comprensión a la hora de exponer algún resultado o exposición.

Luego de eso el licenciado paso a explicarnos algunos de los gráficos mas usuales: 

Explico algunos gráficos, como sus características que los diferencian.

Además de eso nos explico algunos ejemplos de uso de los gráficos para complementar la lección del día.

El tema me pareció bastante familiar y bueno para repasar los diferentes tipos de gráficos, y cuales son mas apropiados dependiendo el contexto, y como existe una gran variedad de opciones para realizar un grafico llamativo y creativo a nuestro gusto.

Alguna recomendación o idea para aprender el tema seria uso de aplicaciones online o de uso de programas como Excel, ya que en Excel existe gran variedad de gráficos y se puede llegar a entender las características de cada grafico, y como ordena los gráficos.

-EJ

r INTERPRETACIÓN DE GRÁFICAS CIRCULARES

SESION 3 Jueves 09/06/2022

¿Lo has utilizado anteriormente?

 

Es una de las maneras más fáciles y prácticas para que puedas demostrar el porcentaje que deseas y así poder captar la atención del mayor y menor ingreso..

¿Cómo podemos solucionar un problema si resulta que hay que relacionarlos y obtener una respuesta sin detallar mas que el porcentaje?

Simplemente debemos de ayudarnos con los pasos de POLYA, y ver que proceso y analizar cual nos ayudara con mas eficiencia a poder obtener un resultado correcto....

A continuación te presento un problema, si ya tienes conocimiento puedes dejar la respuesta de cualquiera de los 4 incisos

💅💜 DG

Martes 7 de Junio, 2022

 Disposición Espacial 1: Tangram

Es un Juego Chino, que consiste en armar formas de animales o cosas, con figuras geometricas: el cuadrado, triangulos y romboide, son 7 figuras en total, siendo 1 cuadrado, 5 triangulos, 2 grandes, 1 mediano y 2 pequeños, tambien el romboide o paralelogramo. El Tangram es un rompecabezas que segun los expertos mejora el rendimiento intelectual de todos los que lo realizan, tanto niños como adultos. 

 - Ejemplo: 

Se trata de analizar cuidadosamente la posición de cada figura.

Disposición Espacial 2: Ladrillos.

Al igual que Tangram, se trata de formar figuaras distintas con la diferencia que son ladrillos o bloques los que se utilizan. donde involucra las habilidades cognifivas del ser humano, donde se debe analizar cual es el espacio correcto de cada pieza, y ninguna puede montar a otra. 

 - Ejemplo: 

 

Clase Martes 6 de Junio, 2022

Inteligencias multiples

La teoría de las inteligencias múltiples es un modelo de entendimiento de la mente elaborado por Howard Gardner y publicado en 1983. Para él, la inteligencia no es un conjunto unitario que agrupe diferentes capacidades específicas, sino una red de conjuntos autónomos, relativamente interrelacionados.

Inteligencia lingüística

• Se entiende como la capacidad de dominar el lenguaje y poder comunicarnos con los demás es transversal a todas las culturas. Desde pequeños aprendemos a usar el idioma materno para poder comunicarnos de manera eficaz. 

• La inteligencia lingüística no sólo hace referencia a la habilidad para la comunicación oral, sino a otras formas de comunicarse como la escritura, la gestualidad, etc.

Inteligencia lógico-matemática

• Durante décadas, la inteligencia lógico-matemática fue considerada la inteligencia en bruto. Suponía el axis principal del concepto de inteligencia, y se empleaba como parámetro para detectar cuán inteligente era una persona.

• Como su propio nombre indica, este tipo de inteligencia se vincula a la capacidad para el razonamiento lógico y la resolución de problemas matemáticos. La rapidez para solucionar este tipo de problemas es el indicador que determina cuánta inteligencia lógico-matemática se tiene.

Inteligencia espacial

• También conocida como inteligencia visual-espacial, es la habilidad que nos permite observar el mundo y los objetos desde diferentes perspectivas. En esta inteligencia destacan los ajedrecistas y los profesionales de las artes visuales así como los taxistas, que deben poseer un exquisito mapa mental de las ciudades por las que transitan. 

Inteligencia musical 

• La música es un arte universal. Todas las culturas tienen algún tipo de música, más o menos elaborada, lo cual lleva a Gardner y sus colaboradores a entender que existe una inteligencia musical latente en todas las personas. • Algunas zonas del cerebro ejecutan funciones vinculadas con la interpretación y composición de música. Como cualquier otro tipo de inteligencia, puede entrenarse y perfeccionarse. 

Inteligencia corporal y cinestésica 

• Las habilidades corporales y motrices que se requieren para manejar herramientas o para expresar ciertas emociones representan un aspecto esencial en el desarrollo de todas las culturas de la historia. 

• La habilidad para usar herramientas es considerada inteligencia corporal cinestésica. Por otra parte, hay un seguido de capacidades más intuitivas como el uso de la inteligencia corporal para expresar sentimientos mediante el cuerpo.

Inteligencia intrapersonal

• La inteligencia intrapersonal se refiere a aquella inteligencia que nos faculta para comprender y controlar el ámbito interno de uno mismo en lo que se refiere a la regulación de las emociones y del foco atencional. 

• Las personas que destacan en la inteligencia intrapersonal son capaces de acceder a sus sentimientos y emociones y reflexionar sobre estos elementos. Según Gardner, esta inteligencia también permite ahondar en su introspección y entender las razones por las cuales uno es de la manera que es.

Inteligencia Naturista

• Según Gardner, la inteligencia naturalista permite detectar, diferenciar y categorizar los aspectos vinculados al entorno, como por ejemplo las especies animales y vegetales o fenómenos relacionados con el clima, la geografía o los fenómenos de la naturaleza. Esta inteligencia se creo para tomar conciencia de los recursos que la madre naturaleza nos brinda, para que actuemos con responsabilidad.

 Estrategia: plantear y resolver una ecuación

La estrategia de utilizar una ecuación de primer grado para resolver un problema es muy importante, porque muchos problemas de las ciencias, la economía, las finanzas, la medicina y de otros campos se pueden plantear en términos de una ecuación. 

Ecuación Una ecuación es un enunciado que establece que dos expresiones son iguales, en ella se incluyen términos conocidos, variables o incógnitas y signos de operación y agrupación. 

Ejemplo 1: 

Exprese el siguiente enunciado verbal en expresión de forma simbólica: cuatro veces un número aumentado en siente unidades es igual a diecinueve.

 Sea 𝑥 = 𝑒𝑙 𝑛ú𝑚𝑒𝑟𝑜

 Entonces 4𝑥 + 7 = 19 es la solución.

La expresión 4𝑥 + 7 = 19 corresponde de un enunciado de ecuación, esta ecuación no es verdadera para todos los valores de la variable 𝑥. Los valores de 𝑥 que hacen que la ecuación sea verdadera se llaman soluciones o raíces de la misma y el proceso de determinar éstas se conoce como resolución de la ecuación. 

Es recomendable utilizar y aplicar los pasos de POLYA

DG💅💚

ESTRATEGIAS PROPORCIONES Y PORCENTAJES 

Sesión 3, jueves 02/06/2022

https://wordwall.net/es/resource/13708468/porcentaje 

"Ingresa al Link y destaca todo tu conocimiento en cada reto que te presenta y así practicaras y te desarrollaras para lo que a continuación te presentare"

¿QUÉ ES?

Proporción: se le llama proporción a la igualdad de dos razones. Una proporción se puede escribir como a:b; : c:d ( y se lee a es a b como c es a d)

Porcentaje: es un razón en la cual el consecuente es 100.

Razón: es el resultado de comparar dos cantidades y siempre es un número real. En la razón x, y (se lee x es a y), donde a x se le llama p y a y consecuente.

ESPERO ESTES DISFRUTANTO Y ESTE PEQUEÑO APORTE SEA MUY UTIL PARA TI.

DG💖

Jueves 2 de junio. 1 sesión: " Primera Prueba Sumativa " 🤓

 En esta sesión nosotros trabajamos nuestra primera prueba parcial o sumativa, en la cual se nos evaluo de los contenidos que llevábamos hasta ese momento, por lo cual imprimimos formatos de trabajo y usamos una hoja de trabajo para guiarnos en las actividades, la cual estaba en el portal.

Y el formato para resolver los ejercicios fue:

La evaluación puso a prueba nuestros conocimientos y temas adquiridos, pero lo mas importante es nuestra capacidad de lógica y razonamiento para resolver problemas, fue un ambiente de presión y estrés, ya que el tiempo era justo pero algunos problemas requerían de una resolución ( inducción) rápida para ser resueltos, por lo cual puedo decir que fue una evaluación al limite.

Hicimos uso de cálculos y figuras de referencia para resolver los diferentes problemas presentados, por lo cual fue una evaluación con varios procedimientos a realizar, un ejemplo que le puedo dar para que se haga la idea de estos procedimientos fue: 

Diferencia Sucesiva

No tengo comentario alguno en esta actividad, mas que fue una actividad muy completa para nuestros conocimientos impartidos :D.

-EJ